삼단논법 대전제 두 가지
(1) '어떤'이 들어가 있지 않는 전제는 대우가 가능하다.
P → Q ≡ ~Q → ~P
ex) 완도와 강릉이 후보지로 선정되면 여수는 선정되지 않는다. ≡ 여수가 후보지로 선정되면 완도 또는 강릉 중 한 곳이 후보지로 선정된다.
(2) '어떤'으로 묶여있는 명제는 앞뒤가 바뀌어도 상관이 없다.
"어떤 학생은 돈이 없는 사람이다." = "돈이 없는 어떤 사람은 학생이다."
(3) 전제들의 순서는 바뀌어도 상관이 없다.
1. 모모모

- 전제 1: 모든 A는 B다.
- 전제 2: 모든 B는 C다.
- 결론: 모든 A는 C다.
삼단논법 문제 중에 가장 난이도가 쉬운 문제.
그 유명한 소크라테스의 삼단논법인 "모든 사람은 죽는다. 소크라테스는 사람이다. 그러므로 소크라테스는 죽는다."도 이와 같은 논리!!
Ex 1)
- 전제 1: 모든 자전거는 기름을 넣는다.
- 전제 2: _______________________________
- 결론: 모든 오토바이는 기름을 넣는다.
전제 2에 들어가는 명제는 "모든 오토바이는 자전거이다."
2. 모모어

- 전제 1: 모든 A는 B다.
- 전제 2: 모든 A는 C다.
- 결론: 어떤 B는 C다.
전제 1과 전제 2에서 공통의 진술이 '모든'으로 묶여 서로 다른 진술과 연결되면, 결론은 그 서로 다른 진술끼리의 '어떤' 관계이다.
Ex 2)
- 전제 1: 고음을 내는 모든 가수는 잘생긴 가수다.
- 전제 2: 고음을 내는 모든 가수는 가요제 출신 가수다.
- 결론: __________________________________________
결론에 들어가는 명제는 "가요제 출신인 어떤 가수는 잘생긴 가수다."
3. 어모어
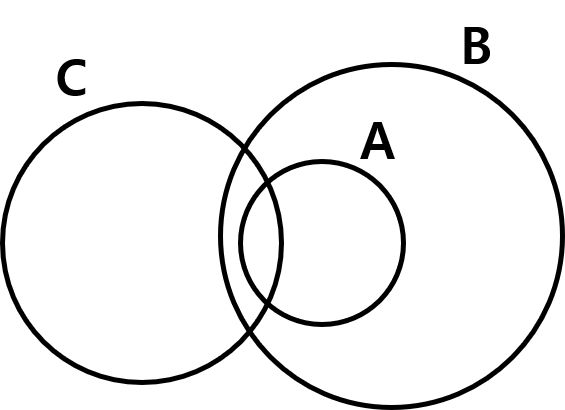
- 전제 1: 모든 A는 B다.
- 전제 2: 어떤 C는 A다.
- 결론: 어떤 B는 C다.
'모든' 관계를 띄고있지 않은 대상이 작은 대상과 큰 대상과 둘다 연결될 경우, 큰 대상과 나머지 대상은 '어떤' 관계.
말이 너무 어렵지만, 렛유인의 GSAT추리 주영훈 선생님은 A를 '작은 애', B를 '큰 애', C를 '(시비)거는 애'라고 표현한다.
그렇게 A, B, C를 '작은 애', '큰 애', '거는 애'로 바꿔보면,
- 전제1: 모든 '작은 애'는 '큰 애'이다. → 큰 애가 작은 애를 감싸고 있음.
- 전제2: 어떤 '거는 애'는 '작은 애'다. → 거는 애가 작은 애에게 시비를 검.
- 결론: 어떤 '큰 애'는 '거는 애'다. → 큰 애가 거는 애를 막으러 옴.
... 이런 느낌??
Ex 3)
- 전제 1: 음악을 전공한 사람은 예술을 좋아하지 않는다.
- 전제 2: ______________________________________________
- 결론: 예술을 좋아하지 않는 어떤 사람은 사진을 취미로 한다.
전제 2에 들어가는 명제는 "사진을 취미로 하는 어떤 사람은 음악을 전공했다."